 |
surfresearch.com.au
surfriding
dynamics
|
fundamental dynamics of surfriding
| home | catalogue | history | references | appendix |
 |
surfresearch.com.au
surfriding
dynamics
|
INTRODUCTION
While it is not necessary to
scientifically understand the dynamics of surfriding to
successfully perform the activity, a basic appraisal of the
process may mariginally increase the surfrider's appreciation of
the art.
It is important to initially
distinguish the difference between riding on the face of a
breaking wave and riding the resultant foam or the white-water
wave (a wave of translation).
Such an analysis must examine the
mechanics of the breaking wave.
Secondly, to eliminate secondary
propulsion forces, this account is based on the dynamics of a standard
surfboard, approximately 8ft x 22'', ridden in a standing
position.
Body, bellyboard, kneeboard and
sufski surfriders often kick and/or paddle to increase
propulsion when there is a decrease in wave power and this can
significantly complicate the analysis.
Given the extreme, possibly inexplicable, manoeuvres demonstrated by modern surfriders, the analysis should similarly be limited to a range of, relatively, low-skill standard or basic functions; the take-off, trimming, stalling and turning.
Finally, the analysis must not only
describe the motion of the surfrider down the wave face and
directly towards the beach, but the more complex traversing
process whereby the ride is at an angle to the wave face.
As such the rider travels faster than
the wave speed, as expressed by Caton- the "astonishing
velocity along the foot of the wave".
1.the mechanics of the breaking
wave.
1.1 Overview
1.2 Breaking wave face
1.3 Wave of translation
2. The Standard Surfboard
2.1 Overview
2.2 Standard Surfboard
2.3 Other Surfcraft
3.motion of the surfrider down the wave face
4.Comlex w
5. traversing
5. Wave of translation
6. Advanced manoeuvres
1.2
This appears to be the case for
ancient Hawaiian surfriders as reported by John Dean Caton:.
"The bathers themselves were
unable to explain what it was that propelled them with such
astonishing velocity along the foot of the wave, and I have
conversed with a lawyer of distinction now practicing in this
country, who was born and brought up at Hilo, and was himself
a successful surf bather.
He could only say that the
propulsion was by the action of the water, which, indeed, was
very
manifest, but 'how' he would not
venture an opinion."
Caton's account above is paraphrased by Tom Blake in his seminal Hawaiian Surfboard (1935), but his source may have not been a complete copy of the book, for he claims:
"Caton found the natives could
not explain why they were propelled shoreward with such
astonishing speed, nor could Mr. Caton explain it
himself, nor could my friends.
He hoped that someday, someone
would study the question and find an answer to it." (6)
"The inclination of the board to
climb up the acclivity - if, indeed, such is the case - when
the wave is
rolling towards the bather, and so
producing a current downward, seems contrary to what we should
expect.
This propulsion parallel with the
wave, I think, only occurs when a comb is breaking on the top
of the
wave, and then it is that the foot
of the wave in front is most distinctly defined, while the
unbroken
swell is very irregular and much
deformed.
That there is a rapid current
rushing along at the foot of the wave at right angles to its
general course I cannot believe.
A block of wood thrown in where
the bather started would no doubt simply rise up over it and
be left
behind to again surmount the
succeeding wave, much less would it dart off almost like a
flash and
maintain its position in front of
the wave.
The only solution to the problem
which I will venture to suggest is, that by placing the
bathing-board
at a certain angle to the
direction of the moving water in the wave an impetus is given
to it in a
direction not in accord with the
impelling force, as by trimming the sails of a ship, so that
the wind will strike them obliquely the vessel is propelled in
a direction different from the course of the wind.
If the results were more marked
than we should expect from the cause suggested, I may say that
we
are not sure that we are
acquainted with the force and direction of all the currents
which accompany a wave of the sea.
At all events, I hope that what I
have said will induce others more competent to study the
subject, and
give a more satisfactory
explanation of the striking facts which I have detailed.
I do not think it will prove more
difficult of explanation than is the action of the boomerang
from the
hands of the Australian native."
Attempts to analyse surfboard
dynamics in the early 20th century have not always greatly
advanced our understanding.
For example, continuing the
above narrative Blake goes on to suggest a, not altogether
satisfactory, solution ...
The answer is relatively
simple. Gravity does the trick.
The front slope of the wave on
which one slides presents a down-hill path, while the
friction of the
slippery board against the
water is very small. (7)
It's the same as skiing on a
snow-covered hill, and there is no doubt as to what makes
one slide down
a hill on skis.
However, in skiing, one can
start down hill from a stationary position, while in
surfriding some
momentum must first be attained
, to catch up with the incoming swell.
This is accomplished by
paddling the board with the hands and arms. (8) - Blake(1935) page 43.
7. "the friction of the
slippery board against the water is very small"
My physics is a bit rusty, but I
think that the friction on the board is significant - otherwise
the board would sink.
More work/thought required.
8. "to catch up with the
incoming swell ... by paddling the board with the hands and
arms."
One of the most common
misunderstandings by surfriders - technically the wave "catches"
the rider.
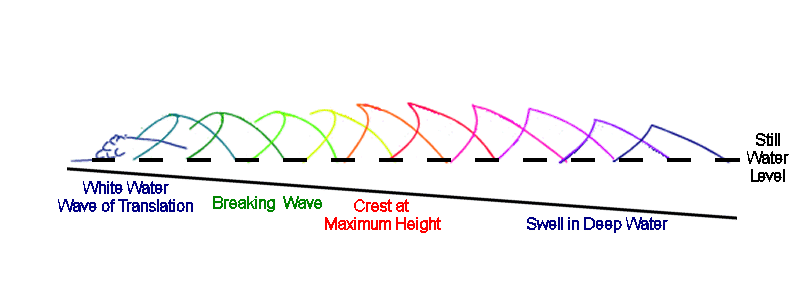 |
|
Wave of Translation |
|
|
Shoulder in Deep Water |
Although surfboard design is not studied in this book, they are planing hulls and several principles expounded by Lindsay Lord appear applicable...
7.1. "hydrostatic
naval
architecture is not applicable to the planning
hull...The fundamental hydraulic laws upon which standard
naval architecture proceedures are based simply do not
apply to a hull skimmimg the surface."
Preface, Page
vii
7.2. "the
submerged
body, moving with sufficient rapidity, increases
turbulence and the resulting suction drag, soon reaching a
speed at which the viscosity of the liquid prevents
further increase in speed regardless of practical
increases in power.
With the
plate (surfboard) moving in its own plane, this
type of suction drag due to the viscosity of the liquid is
not a factor in the performance.
Rather,
the resistance, aside from skin friction, is largely due
to the simple transfer of kinetic energy at the leading
edge.
Thus it
becomes apparent that the leading edge of the plane at
once accounts for a major portion of both drag and lift.
But since
lift rises as the square of the speed, and drag increases
at less than the square of the speed, every proportionate
increase in leading edge increment becomes successively
more and more worthwhile.
In other
words, while increasing speeds require the displacement
hull to become progressively narrower, the planning hull
moving at high speed requires the widest possible beam.
To
simplify still further, the displacement hull can improve
its speed only with added length; the planning hull
requires added beam."
Pages 12 - 13.
7.3.''With
planning
hulls, then, there is no theoretically sound procedure by
which the total resistances of one hull can be directly
compared to the total resistances of another hull
radically different in size."
Page 25,
follows analysis of Froude's Law of Comparison and the
Reynolds number.
7.4 ''Unfortunately,
airfoil
or hydrofoil data is of limited value as an approach to
this problem (of bottom loading).
The
boat's (surfboard's) bottom operating at the
boundary between two mediums, one of which is
approximately 800 times as dense as the other, allows but
for one working face of the plane.
Furthermore,
while
this one face should ideally be subjected only to positive
pressures, certain configurations of the average bottom
lead to varying degrees of transient negative pressures
which may detract from the net dynamic lift of the plane."
Page 31.
Note that this
does not apply to fins, which are true hydrofoils.
|
Board C
6 ft x 22'' Wf = f g |
Board B
8 ft x 22' Wf = f b |
10 ft x 22'' Wf = f a |
 |
 |
 |
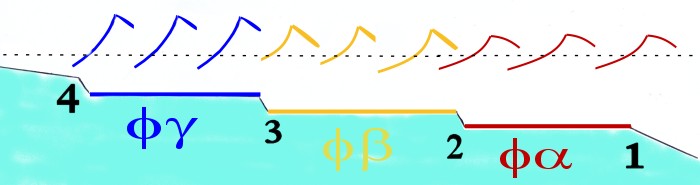
i. The board accelerates down the
face towards the trough.
This will ultimately result in rapid
deceleration as the wave face angle approaches 0.
ii. The rider stalls the board (applies drag) and maintains board speed at wave speed.
iii. The board travels at an angle
to the wave face, the resultant vector being at wave speed.
In this instance potential board
speed is further increased because...
"When the
board cuts or angles across the wave face, natural wave
dynamics cause the leading edge of the board to extend
longitudinally, thereby greatly increasing the board's speed."
(#10. above)
2. Three riders on similar boards take off on a wave at a fixed point (T/O).
3. No board's wake effects the other riders.
4. Rider #1 takes off (T/O)
behind the peak and turns into the tube at a second fixed
point (T1).
With minor adjustments the surfer
stays inside the tube in a straight line till a third fixed
point (T2).
5. Rider #2 takes off (T/O) on
the shoulder and sets up a bottom turn at the second fixed
point (T1).
With major adjustments the surfer
climbs and drops on the wave face till a third fixed point
(T2).
6. Rider #3 takes off (T/O) on
the wall and walks to the board's nose at the second fixed
point (T1).
With minor adjustments the surfer
noserides in a straight line on the till a third fixed point
(T2).
This is represented graphically...
Observations...
1. Rider #2 rode the longest
distance.
2. Riders 1# and #3 rode a shorter
and equal distance.
Therefore...
Rider #2 has the highest velocity
(v = d/t).
Riders #2 and #3 have the same
velocity !!! - the Analytical Dilemma.
Weirdo...
Tube riding surfers report that
inside the tube "time slows down".
Possibly related to ...
1. Extreme board speed, see above.
2. Visual "tunneling" as predicted
by Al Einstein when approaching the speed of light.
| Lord,
Linsay : Naval Architecture of Planing Hulls Cornell Maritime Press 241West 23rd Street New York 11, N.Y.1946 Hard cover, 305 pages, 21 black and white photographs, 118 black and white diagrams and graphs, Index Review Although surfboard design is not studied in this book, they are planing hulls and severval principles expounded by Lindsay Lord appear applicable. The book was treasured by seminal Californian board builder, Bob Simmons. Many of the models and diagrams appear similar to Simmons' famous wide tailed Spoons of the early 1950's, Lord emphasizing the increase in lift by incorprating parallel running lines, page 71. |
 |

| Kinstle, James : Surfboard Design and Construction Natural High Express Co. Long Beach, California.1975 Soft cover, 139 pages, extensive black and white illustrations and diagrams. Image This is not an original, but a photocopied version contributed by A. -thanks to A. Review 1. Probably the most technically detailed work on surfboard design ever published, many sections are unique. It would be unfair to attempt a critical review at this point since I don't feel that I fully understand much of the work, in particular Chapter 2 Surfboard Dynamics. 2. October 2004 |
 |
 Kit Horn, Bob Simmons and Buzzy Trent. Solid Laminates, Malibu, circa 1941 - 1944. Surfer Magazine March 1981 Volume 22, Number 3, page 36 The photograph is uncredited. |
 Planing surfboard tail. Photo by Michael Peterson, 1973. |
|
Kuhio Pier, Waikiki, circa 1962 Photograph by Val Valentine Kelly, facing page 192. |
 |


| home | catalogue | history | references | appendix |
The History
I checked the
entry for 1902 in Chronicles of the 20th Century, Viking Press
(1999), page 52 (I think, but unfortunately not at hand) and
note:
1. It adds no
new information to the story.
2. Is without
specific references.
3. The book
itself appears to be general in nature and in some places is
less than accurate.
I cross checked
with the entry for the 1964 World Surfing Championships at
Manly NSW (about page 106) and noted several discrepancies.
Apart from
Curby, regretably I do not have a copy of the one serious work
that should (if pertinent) report the activities of Gocher ...
Champion,
Shelagh and George: Bathing, Drowning and Life Saving in
Manly, Warringah and Pittwater to 1915.
14 Tipperary
Avenue, Killarney Heights NSW 2087
Published
and printed by Book House, Glebe, 2000.
I have requested a copy by inter-library loan, but these can take up to four weeks before the item is available.
The Fluid
Mechanics
Please note
that even basic physics is testing my intellectual
capabilities and any comments are offered with less than 100%
confidence.
Firstly, I
feel we may be approaching the question from somewhat
different perspectives.
You appear to
largely base your analysis on body surfing and surf life
saving race and/or rescue events.
My view is
focused more on surfboard riding.
My focus is
not just a personal preference - I would suggest that
while all surfriders essentially replicate similar dynamics,
the standing surfrider's motion is essentially dependent on
the motion and structure of the wave.
Body surfers
(in addition to the ability of skilled practitioners to make
substantial variations in their body shape and in their
buoyancy) often kick and/or paddle while riding on the wave to
supplement the wave propulsion when there is a decrease in
wave power to maintain or improve their position on the wave.
Similarly for
bellyboard, kneeboard and sufski riders.
This is most
evident in the surfriding performance of sail and kite
boarders.
These
supplementary applications of force could significantly
complicate the analysis.
Furthermore,
for surf life savers when attempting a rescue or racing in
competition the preferred course is (usually) a direct line to
the buoy/patient and back to the beach.
Waves are then
ridden the shortest distance straight to the beach.
For the
surfboardrider the object is to ride transversely across the
wave face, thereby maximising the length of the ride.
In your example
of "using a boogieboard, surf-o-plane or other craft" which
"proceed some distance ahead of the broken surf front. But
then it catches up with one and it is then difficult sometimes
to stay in control", the experienced surfrider avoids this
situation by directing the board transversely (either left or
right) and continues to ride on the much more controllable
green breaking wave face.
It is likely
the dynamics of this transverse motion are somewhat more
complex that proceeding directly to the beach.
To illustrate
one potential analytical difficulty between these two
perspectives:
"one can catch
and ride a broken wave on a sandbank"
The "breaking
wave" and the "broken wave" are two different hydrodynamic
entities.
In the former,
the water transcribes increasing elliptical obits as it
approaches shallow water and breaks when the obit is broken by
friction with the bottom.
The movement of
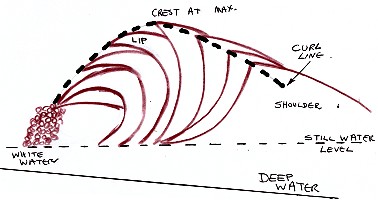
water in a breaking wave is highly complex (illustration
below) but until the crest approaches its maximum height, the
resultant motion of the water towards the beach maybe
relatively minor.
"when waves are
steep the orbital circles of the water particles do not
exactly close.
The water
itself is transported by the passing wave form, although its
progress is very slow compared to the wave velocity."
Bascom,
Willard: Waves and Beaches
Anchor Books
Doubleday and
Company Inc.
Garden City,
New York 1964. , pages 38 and 39 and image below, page
40.
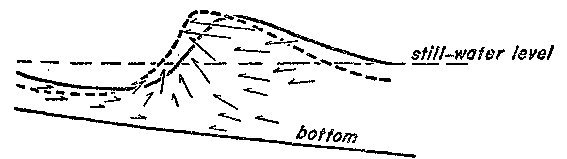
"FIG. 14.
Movement of water particles as a wave breaks in wave channel
(from motion picture analysis)."
Note that while
most water particle movement is shoreward, there is
significant water movement
seaward
(from the trough) and up vertically up the wave face.
As large
surfcraft (boards and skis) can catch and ride the wave well
before the wave crests ("runners") it would appear that this
motion may not be dependent on "the forward drag force exerted
by the water particles."
Certainly once
the wave has passed the point of maximum crest height, and the
crest now becomes "the lip", there is a massive forward
movement of power and water.
This results in
the broken wave, the white-water or "a wave of translation"
[Bascom (1964), pages 160 and 161].
Now a wall of
aerated water, without the discernable wave face or the
characteristic trough of the breaking wave, it moves enmass
towards the beach.
In most cases,
a riderless bouyant object located anywhere inside the
breaking wave zone will be easily caught by the white-water
and carried swiftly shoreward.
This basic
motion is commonly and effectively used by riders of highly
buoyant inflatable surfo-planes or surfmats.
For green breaking waves the situation is almost the reverse - a riderless bouyant object moving towards the beach from deep water (say propelled by a very light onshore wind) will simply rise and fall with the passing of the swells and only is lauched rapidly shoreward when positioned at a critical point of on the face of a breaking wave.

|
Wave of Translation |
|
|
Shoulder in Deep Water |
Page 126
SURFING ON
WAVES
Surfboards,
small craft, and animals (including porpoises and
body-surfers) can take energy out of the waves to propel
themselves by sliding down the forward surface of an
advancing wave.
The
surfboard is thrust forward by a downhill force or slope
drag, shown in Figure 46 as a vector connecting the gravity
force to the buoyancy force (which always acts perpendicular
to the water surface).
When the
slope drag is greater than the hydrodynamic drag (water
resistance) the object moves at wave-crest speed.
The trick of
surfing, of course, is to get the board moving and the
weight properly balanced so that the slope drag can take
over the work of propulsion at the moment the wave passes
beneath.
If the surf-
board is also moving sidewise across the face of the wave,
it may move at a considerably higher velocity than the wave
itself.
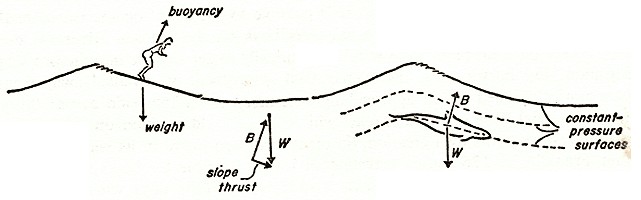
Figure Page (adjusted)
Dukws-
amphibious trucks used for surveying the surf zone-not only
can assume the proper slope, but also can also take
advantage of an additional effect to "surfboard" on large
breaking waves.
Their front
axles hang down so as to offer a vertical surface for ...
FIG. 46.
Slope thrust drives the surfer and the porpoise. (after
Harold Saunders)
(Adjusted)
... the
orbiting water particles to press against.
Body-surfers
who hold their hands down beneath their bodies can get the
same kind of boost.
The air-water interface is a surface of constant pressure; beneath it are other parallel surfaces of constant pressure that move with imaginary waves that are subsurface reflections of the visible waves above.
Porpoises
are neutrally buoyant and with a little practice learn to
tilt themselves at the proper slope to take advantage of the
slope drag to surfboard on some underwater constant-pressure
surface. These animals can ride beneath the bow wave of a
ship indefinitely without appearing to exert any effort at
all.
Apparently a
porpoise can do this because the skin drag of his curious
hide is less than the slope drag on the invisible surface.
It is
possible to surfboard on the waves made by a ship.
As boys on
the Hudson River we used to paddle frantically to get a
canoe into the proper position behind a ferryboat as it
pulled away from the pier so we could get a free ride across
the river, merely steering to hold position on the steep
slope of the first transverse wave in its wake.
And it is
also possible for boats to surfboard on their own waves.
In the days
when canal barges, drawn by horses on a towpath, were widely
used for transportation, the horses soon discovered that if
they temporarily speeded up on approaching a narrow stretch
of canal, they could then relax while the boat rode the
waves of its own creation.
So reported
Benjamin Franklin in 1768 after traveling on the canals of
France.
Many years
later Scott Russell studied "fly boats" on the Scottish
canals where the same "advantageous principle was employed
to reach high speeds in the passenger trade."
The canals
were very shallow (probably less than four feet) so that the
waves moved at (the square root of) gd velocity or about ten
feet a second (7 mph).
One can
imagine that when the canal suddenly narrowed and the height
of the bow wave increased, a wise horse (or driver) would
smile to himself at the prospect of surfboarding his load
for a while.
Bascom (1964),
pages 126 to 128.
1. Slope Theory decribes surfriding dynamics on the face of a breaking wave and not on the broken wave of translation.
2. It appears
to be applicable to all surfriding methods - from the
unencumbered body surfer to a 30 foot outrigger canoe.
Furthermore, it
is also applicable to wave riding of porpoises and, by
implication, seals.
When riding a
wave, experienced seals can alternate between underwater
constant pressure forces (like a porpoise) and the breaking
wave face (like a human bodysurfer).
3. Slope Theory essentially describes the the point where the surfrider achieves take-off, that is moving at wave speed and dependent only on the forces of the wave.
4. The determining factor in successful surfriding is a direct relationship between bouyancy and the slope of the breaking wave face.
Therefore,
larger (more buoyant) craft achieve take-off at a (relatively)
slight wave face angle.
This is often
at a considerable distance before the wave breaks.
Conversely,
smaller craft require a steeper wave face angle to achieve
take-off.
This is usually
very close to where the wave breaks.
This variation
is often simply observed at popular beaches.
If viewed from
the side, for example at a central position on a headland, the
surfriders appear in striated bands based on craft size.
From shore the
surfriders are grouped as inflatables, bodysurfers,
handboards, bellyboards, kneeboards, small surfboards (6ft),
standard surfboards (8ft), large surfboards (10ft), surfskis
and furtherest out to sea, surfboats.
5. Surfriding is dependent on wave shape and not, although it is certainly enhanced, by wave size, wave speed or wave power.
6. Slope
Theory does not require that the rider "paddles onto the
wave", the essential factor is to postion the surfrider at the
critical take-off point.
This importance
of critical postioning is illustrated by the "no paddle
take-off"
"You can
then do some expert shooting.
For
instance - instead of swimming to pick up the wave, wait
for it to come to you and, as you are
being
lifted, swing the body round and forward.
If you
have timed this movement correctly, the wave will do the
rest."
Hay, Harry: Swimming
and
Surfing.
Jantzen
(Australia) Ltd, Lidcome, Sydney, 1931, page 12.
As a surfrider paddles (or swims) significantly slower than the wave speed, in a sense they do not catch the wave - rather the wave catches the surfrider.
7. While it
may appear minor in the context of Bascom's large picture
analysis, he does not note the importance of wind conditions
to the surfrider.
In onshore
winds the board speed will be slightly diminished due to the
surface chop and the wave will break earlier than if dependent
of the bottom contours.
Once broken,
it's rate of peel, or the curl speed, will be erratic (see 8
below).
In no-wind
conditions the board will travel smoothly, and the breaking of
the wave will depend on the bottom contours.
In mild
offshore winds surface chop will be largely negated by the
action of the breaking waves in the opposite direction and
surface conditions on the wave face may resemble no-wind
conditions.
This wind will
tend to hold up the wave face and delaying breaking.
8. Bascom,
without considering further, notes:
"If the surf-
board is also moving sidewise across the face of the wave, it
may move at a considerably higher velocity than the wave
itself."
He does not
give a detailed account of the dynamics of the wave face as it
breaks transversely, a characteristic highly valued by
surfriders.
For
surfriders, the longest and clearly defined transversely
breaking waves are at point breaks where the swells align at
approximately 90 degrees to the shoreline along the point.
Famous
Australian examples include Byron Bay in NSW and Rainbow Bay,
Queensland.
In California,
Malibu Point.
In the case of the point break, a three dimension image of the bottom contours, and the resulting breaking wave pattern, can be conceived as a conjunction of the illustration above showing the progressive wave structure towards the (actual) shoreline and the same image, now static, rotated 90 degrees where the unbroken wave in deep water is now seen as the wave "shoulder".
In nature,
this perspective most resembles a concave spiral vortex,
uniquely in the case of the breaking wave, in a horizontal
plane.
Vortexes were
of particular interest to Leonardo da Vinci.
"The peculiar form and efficacy of circulatory force in a vortex came from what he (da Vinci) called 'a circumstance worthy of note'; 'The spiral or rotary movement of every liquid is so much the swifter as it is nearer the centre of its revolution', unlike a wheel in which the movement 'is so much slower as it nears the centre' (C.A.296vb)."
Pedretti,
Carlo: Leonardo da Vinci - Art and Science.
TAJ Books, 27
Ferndown Gardens, Cobham, Surrey, KT11 2BH, UK, 2004, page
307.
The concave spiral characteristics of the transverse breaking wave may significantly contribute to transverse motion of surfriders across the wave face.
Perhaps one should also note at this point that these hydrodynamic horizontal concave spiral vortexes can have aesthetic properties, as noted by da Vinci:
"It is not
hard to understand the aesthetic qualities which drew him 'to
investigate the many beautiful
movements which
result from the penetration of one element into another'
(F.34v)."
Pedretti
(2004), page 308.
9. Bascom's
note that a surfboard can move "sidewise across the face",
considered above in respect of wave
dynamics, may
also be further examined in the context of surfboard motion.
It is likely
the dynamics of this transverse motion are somewhat more
complex than the factors that entail
successful
take-off as described by Bascom's Slope Theory.
Some insight
maybe gained in the work of naval architect, Linsay Lord.
Lord, Linsay:
Naval Architecture of Planing Hulls.
Cornell
Maritime Press, 241West 23rd Street New York 11, N.Y.1946.
Lord researched ocean going high speed planning hulls (PT Boats) for the US Navy during World War Two, and he drew a strong distinction between the dynamics of these craft and displacement vessels:
"hydrostatic
naval architecture is not applicable to the planning
hull...The fundamental hydraulic
laws upon which
standard naval architecture procedures are based simply do not
apply to a hull
skimming the
surface." - Preface, page vii.
Lord further illustrated the distinction:
"Unfortunately,
airfoil or hydrofoil data is of limited value as an approach
to this problem (of bottom loading).
The (planning
hull) boat's bottom operating at the boundary between two
mediums, one of which is approximately 800 times as dense as
the other, allows but for one working face of the plane." -
page 31.
I would
contend that a surfboard is a planning hull, as described by
Lindsay Lord.
Incidentally,
the only part of a (modern) surfboard that performs
hydrodynamically is the fin.
A critical factor in Lord's research was the importance of width or beam:
"since lift
rises as the square of the speed, and drag increases at less
than the square of the speed, every proportionate increase in
leading edge increment becomes successively more and more
worthwhile.
In other words,
while increasing speeds require the displacement hull to
become progressively narrower, the planning hull moving at
high speed requires the widest possible beam.
To simplify
still further, the displacement hull can improve its speed
only with added length; the planning hull requires added
beam." - pages 12 and 13.
To speculate,
the transverse motion of a surfboard across the wave face is a
function of the breaking waves conical or spiral structure
(see 8 above).
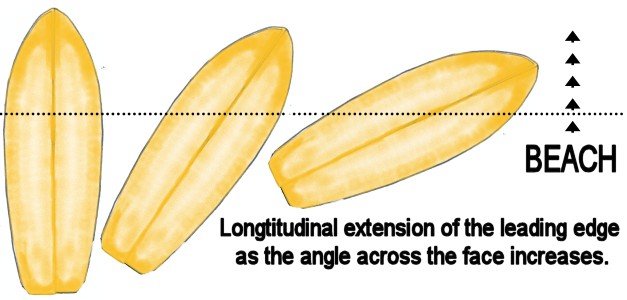
At take-off the
board is traveling at wave speed, the leading edge basically
the approximate width of the board.
When the board
cuts or angles across the wave face, natural wave dynamics
cause the leading edge of the
board to extend
longitudinally, thereby greatly increasing the board's speed.
This is
illustrated in photographs of surfboard riders at high speed
trim on large waves in the marked difference between the point
of breakaway of the wakes from the inside rail (closest to the
wave face) and the outside rail.
